Simulated Annealing
- Gianluca Turcatel
- Jan 15, 2022
- 4 min read

Introduction
Simulated annealing is a well-established metaheuristic, physics-based method that seeks the parameters of a model that maximize (or minimize) the model's objective function.
Simulated annealing is a variation of the simple hill climbing algorithm. You can learn more on Hill Climbing algorithms HERE. The biggest drawback of hill climbing algorithms, such as simple hill climbing and steepest descent hill climbing is that they get stuck at local optima: they are greedy algorithms with very little exploration of the solution space. This deficiency can be partly corrected with multiple restarts, allowing a more comprehensive investigation of the solution space.
Simulated annealing, on the other hand is a stochastic optimization algorithm that explores the full solution space and is better suited to reaching the global maximum. In this article we will code simulated annealing from scratch and implement it to solve a simple maximization problem.
The algorithm
The idea behind simulated annealing comes from the metallurgy field: at high temperatures, the metal is liquid and the metal particles are free to move around; as the temperature decreases metal particles move less and, eventually, stop when the metal turns solid.
In simulated annealing this is translated as accepting bad solutions with high probability at high temperatures and rejecting them at low temperatures. In the implementation, the temperature is an hyperparameter whose value is high at the beginning and is decreased at each iteration: thus, as the algorithm progresses, bad solutions are more and more rejected.
As in other optimization algorithms, the first step is to pick a candidate solution: that becomes the initial current candidate. Next, another candidate is randomly chosen from the solution space and compared to the current candidate based on the value of the objective function: if the new candidate is better, it is accepted and becomes the current candidate. On the other hand, if the new candidate is worse, it is accepted with probability, p given by:

where T is the temperature at the current iteration and DIFF is the difference between the value of the objective function of the two candidates:

In a maximization task, DIFF is negative when the new solution is worse than the current one, which means p will range from 0 (very small DIFF) and 1 (DIFF = 0): the worse is the new candidate, the lower the probability of accepting it. T is the temperature of the system at the current iteration. With very high temperature DIFF / T ---> 0, and p approaches 1, thus bad candidates are accepted easily. When T is very small, DIFF / T ---> -∞, p --> 0 and bad candidates are mostly rejected.
Typically values of T are 90-100 at the beginning and <1 in the last few iterations.
Pseudocode:
Prework: Specify Tmax, Tmin, n_iterations. Set temperature T to Tmax.
Calculate DT = (Tmax - Tmin) / n_iterations
STEP1: Randomly pick a starting point in the solution space and evaluate
the objective function
STEP2: Propose a new solution and evaluate the objective function
STEP3: Calculate the difference (DIFF) between of the objective function
value as defined in (2)
STEP4: If DIFF > 0 --> accept the new solution
If DIFF < 0 --> accept the new solution with probability p as
defined in (1)
STEP5: Reduce the value of T by DT
STEP6: Repeat STEP2-STEP5 for n_iterations (equivalent to T reaching Tmin)
STEP7: Return final solution Implementation
The objective function we will maximize is:

in the interval x = [-8, 20]. The shape of (3) in the given interval is depicted below:

Figure 1. Shape of the objective function
Note the presence of one global maximum, two local maxima and one plateau. The Jupyter Notebook with the complete code can be found HERE. Herein, I will share only the for loop of the algorithm:

Figure 2. Meat of the simulated annealing algorithm
Briefly: inside the loop a new candidate is proposed and tested: if it improves the value of the objective function, is accepted and becomes the current candidate solution. Otherwise, it will be accepted with probability given by (1). At the end of each iteration, the temperature T is decreased of DT (cooling of the system).
In this tutorial we seek to maximize the objective function: therefore, we seek a positive value of the variable diff in order to accept a new solution; if the goal is to minimize the objective function, we will accept new candidates for which diff is negative and, we will flip the sign of diff in (1) when the new candidate is worse than the current one.
Running the simulated annealing algorithm for 600 iterations is sufficient to discover the global maximum:

Figure 3. Simulated annealing algorithm - results
The animation below clearly shows that with high temperature the algorithm is searching through out all the solution space. However, when T is small, the search concentrates nearby global and local optima.
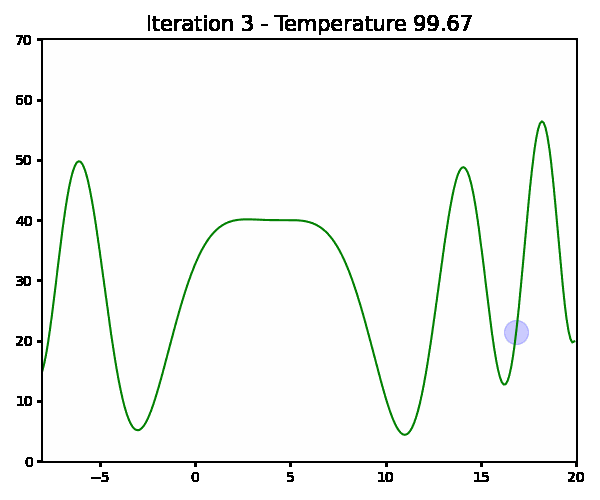
Figure 4. Simulated annealing algorithm - search path
The simple hill climbing algorithm will often get stuck at a local maximum. If you take a look at my article (HERE) on simple hill climbing (where the same objective function was maximized), you would notice that, in only 6% of runs (Figure 8 of the link) the global optimum is found. The reason is depicted below:

Figure 5. Interval that will lead simple hill climbing towards the maximum
Only a small portion (blue bar) of the whole solution space can take simple hill climbing to the global maximum. Simple hill climbing is not a stochastic algorithm and only analyzes neighboring states of the current state: therefore if the initial candidate falls outside the blue interval, simple hill climbing cannon find the global maximum. In contrast, simulated annealing has no search boundaries and it does not focus on testing neighboring states (actually, there are no "neighbors" in simulated annealing, the whole solution space is the neighborhood): therefore, simulated annealing is more able to converge towards the global optimum.
Concluding remarks
In this tutorial you learned how to code and implement simulated annealing from scratch, and the basics of why it outperforms other naive hill climbing algorithms.
Комментарии